
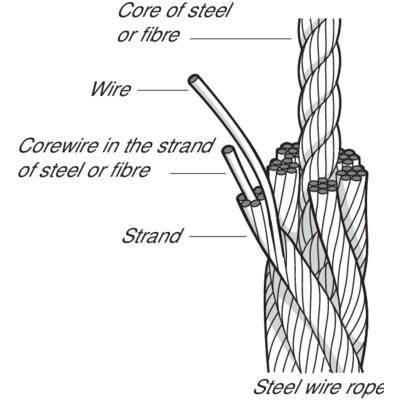
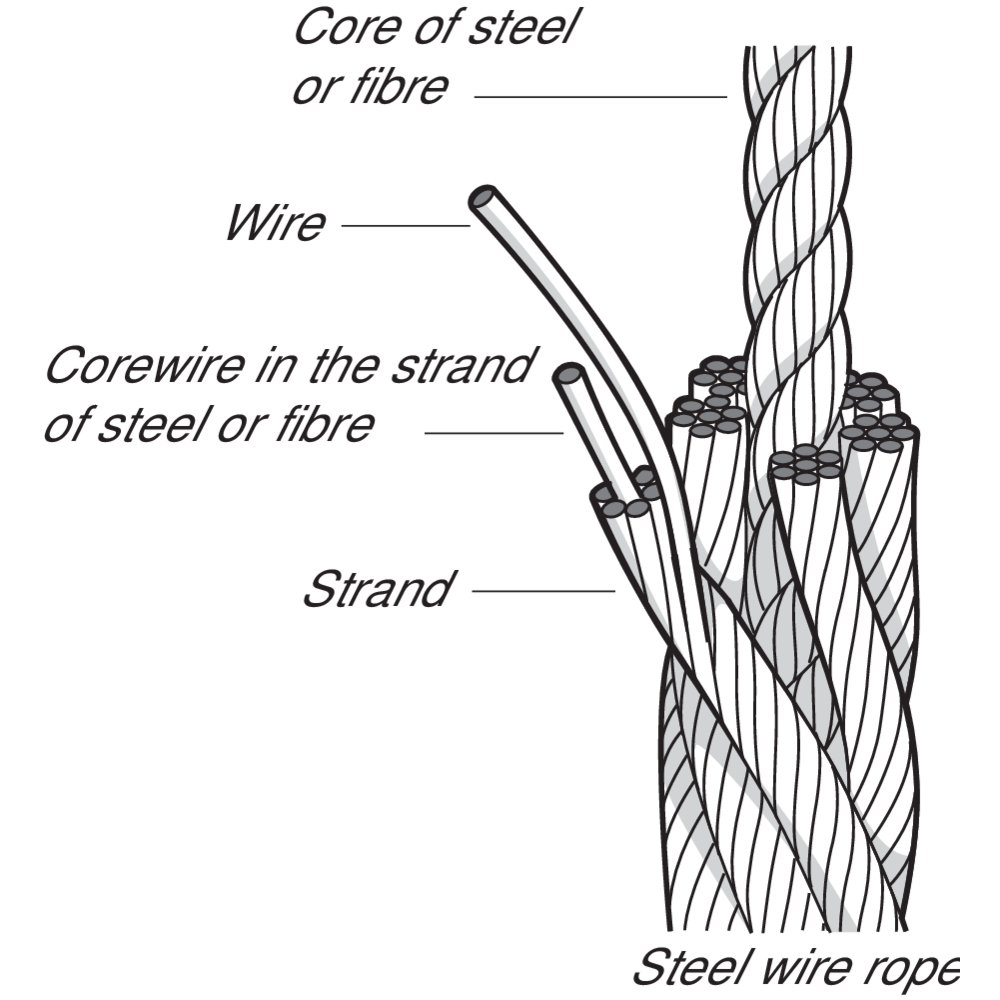
Steel wire rope construction
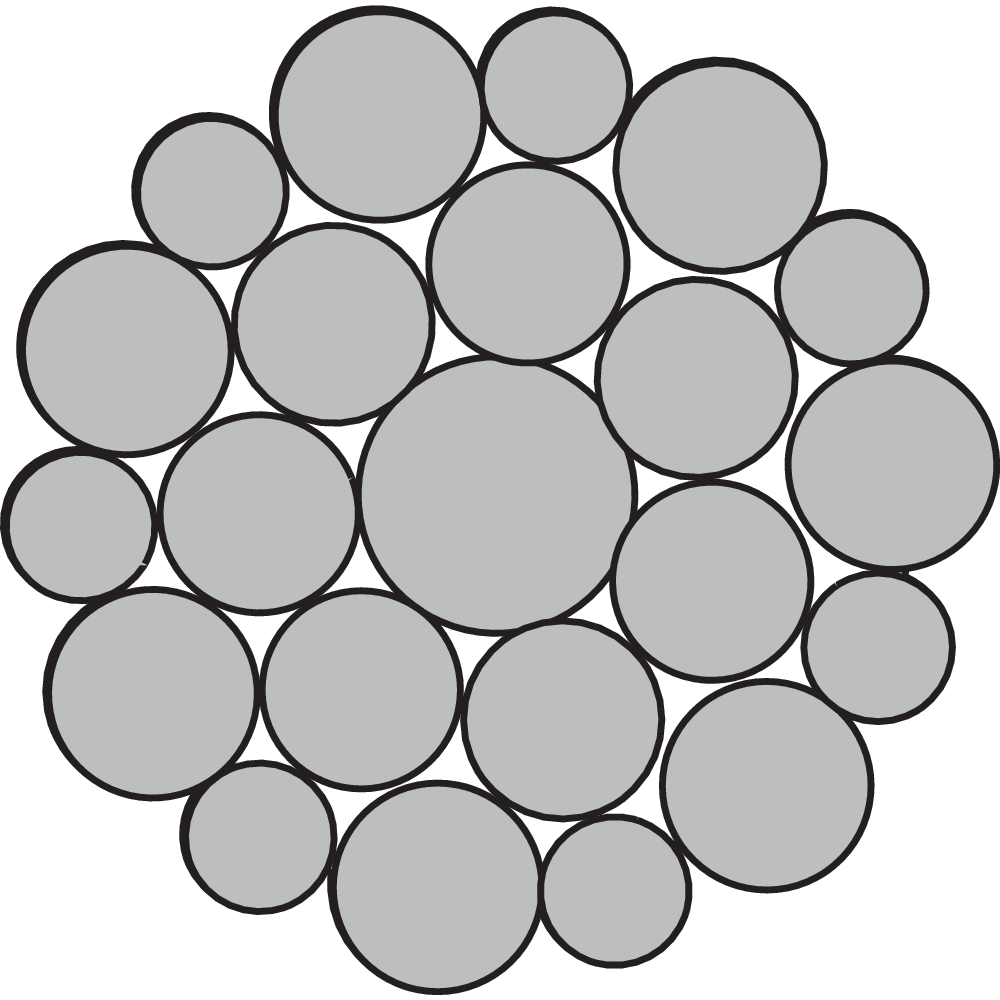
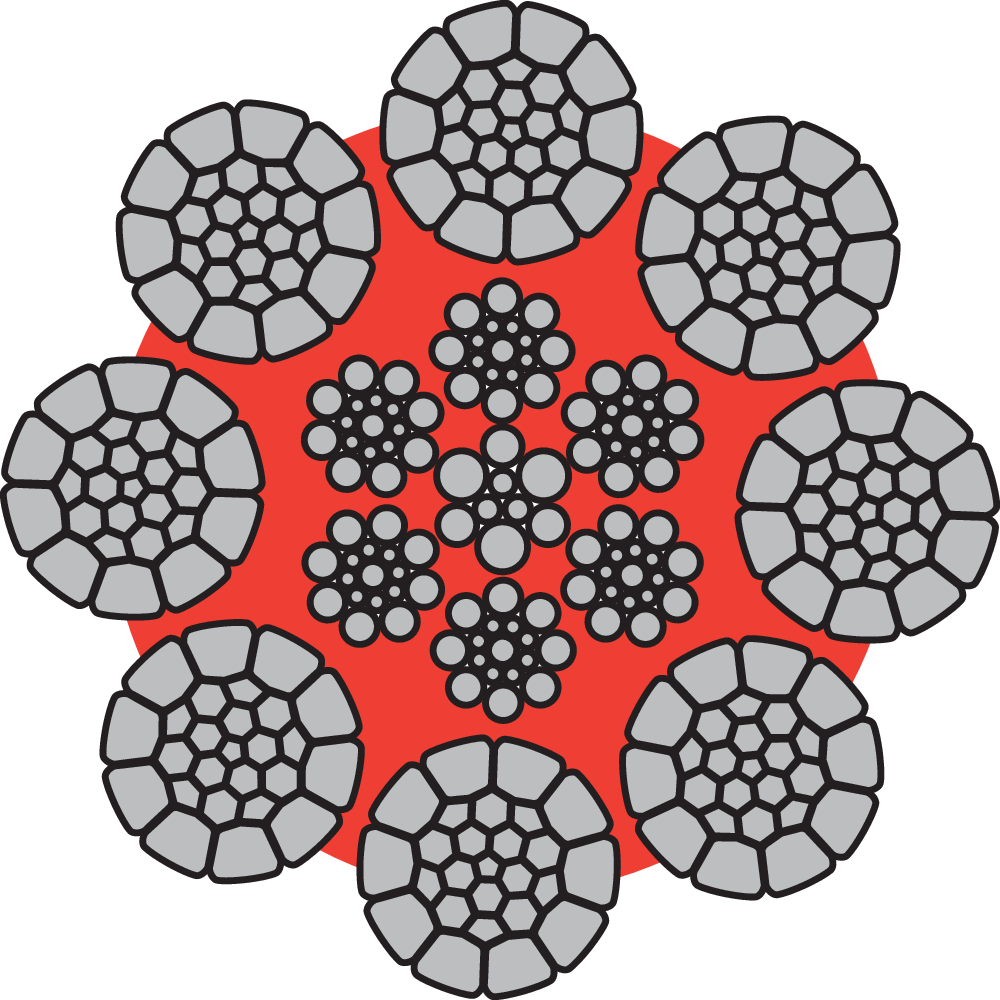
A steel wire rope is made up of individual steel wires spun into a strand. A number of strands are closed over a central core to make up a rope. The number and size of wires will determine the best compromise possible between large wires for maximum corrosion protection and resistance to abrasion, and smaller wires for the required flexibility and handling.
The construction of a steel wire rope is expressed according to the following:
e.g 6x36-FC
6 is the number of strands in the steel wire rope
36 is the number of wires in the strand
FC is the type of the core

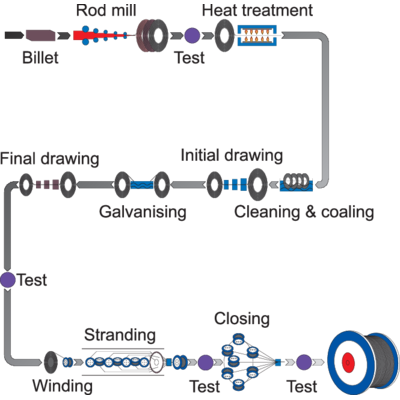
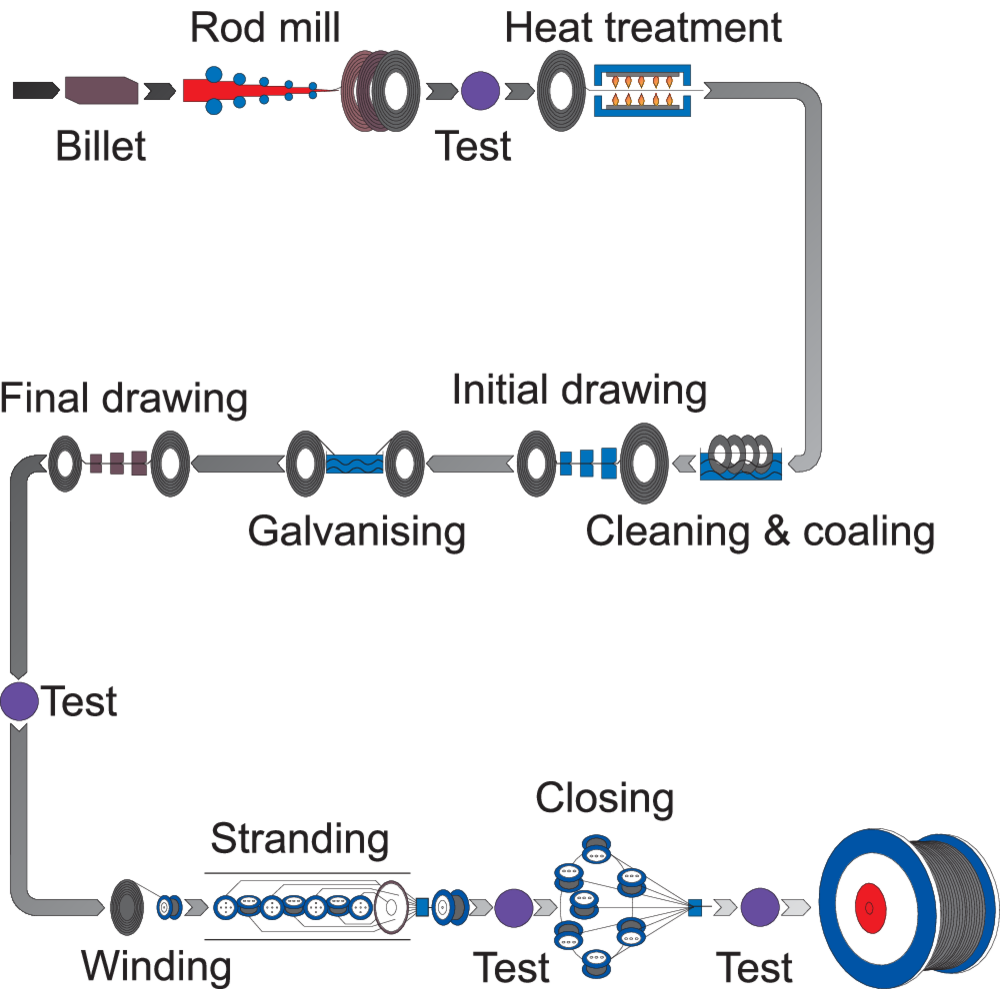
From Rod to Rope
Steel wire rope production process from rod to rope

Steel wire rope grades
The basic material is wire rod, which is cold-drawn into wire of different diameters and strength grades.
The most common grades are:
|
Rope grade |
Wire tensile strength grades |
Hardness app. |
|||||
|---|---|---|---|---|---|---|---|
| EN | API 9A | Min | Max | Brinel | Rockwell | ||
| kp/mm² | N/mm² | kp/mm² | N/mm² | HB | HRC | ||
| 1570 | PS | 140 | 1370 | 180 | 1770 | 405/425 | 45 |
| 1770 | IPS | 160 | 1570 | 200 | 1960 | 445/470 | 49 |
| 1960 | EIPS | 180 | 1770 | 220 | 2160 | 70/480 | 51 |
| 2160 | EEIPS | 200 | 1960 | 220 | 2160 | 480/500 | 52 |
Finish
The wire is either untreated (bright), galvanised or stainless. Galvanised wire gives the rope greater protection for corrosive environments. For extreme cases a stainless rope is used. Steel wire ropes can also be provided with plastic impregnation.
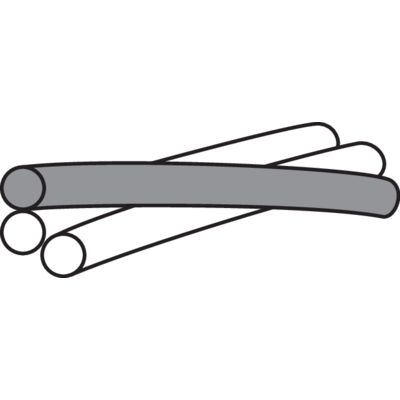


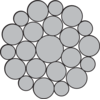
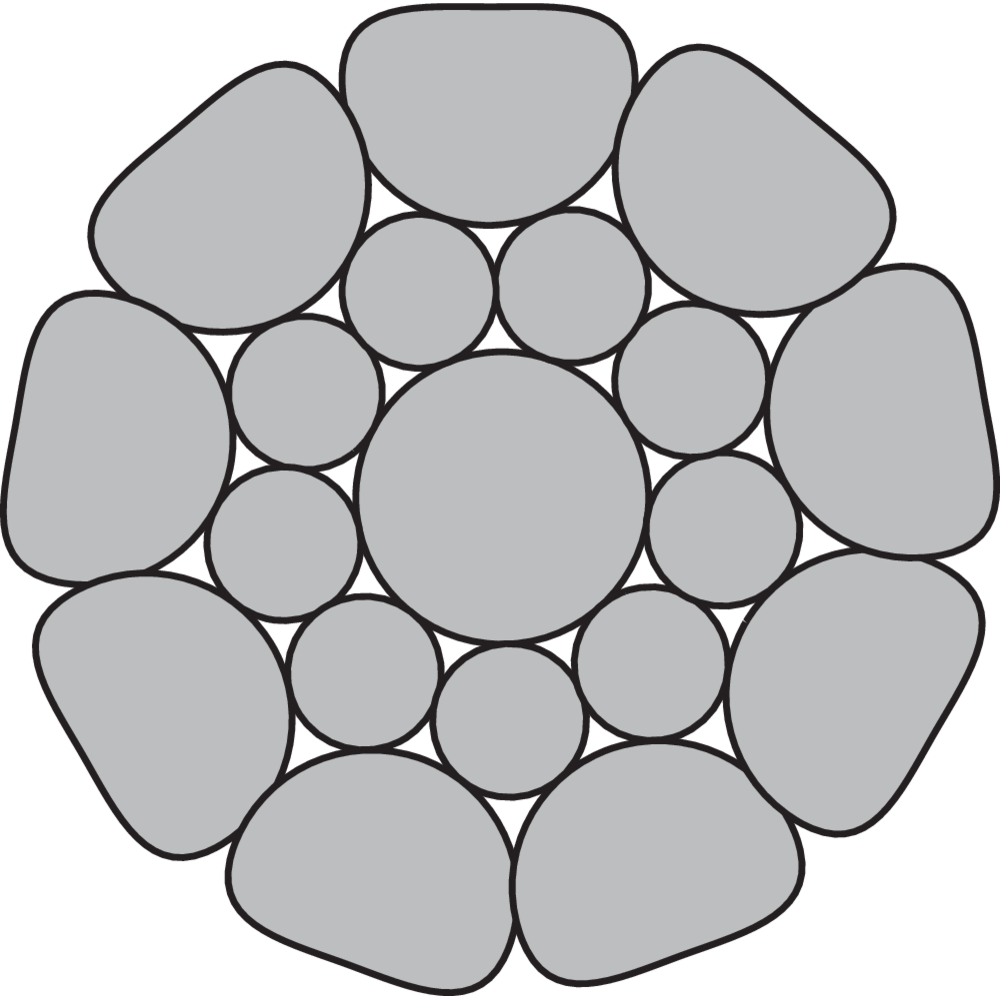
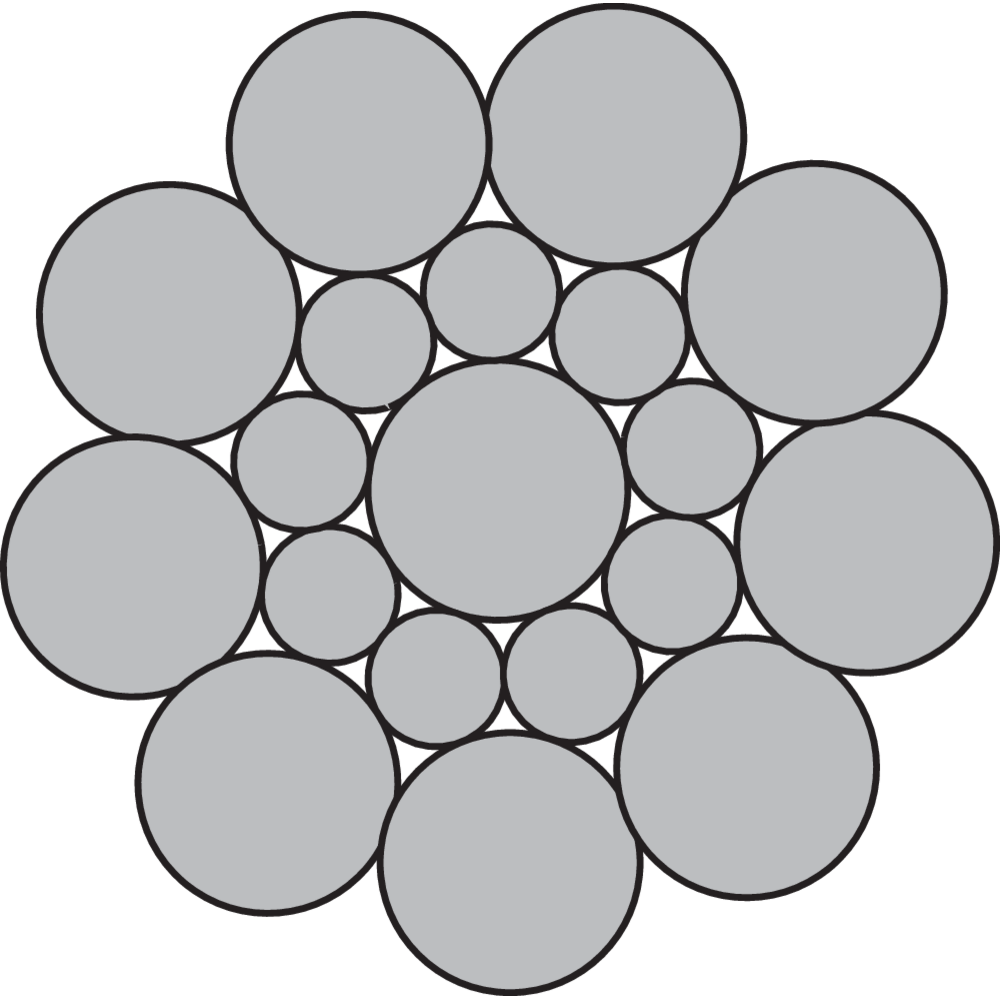
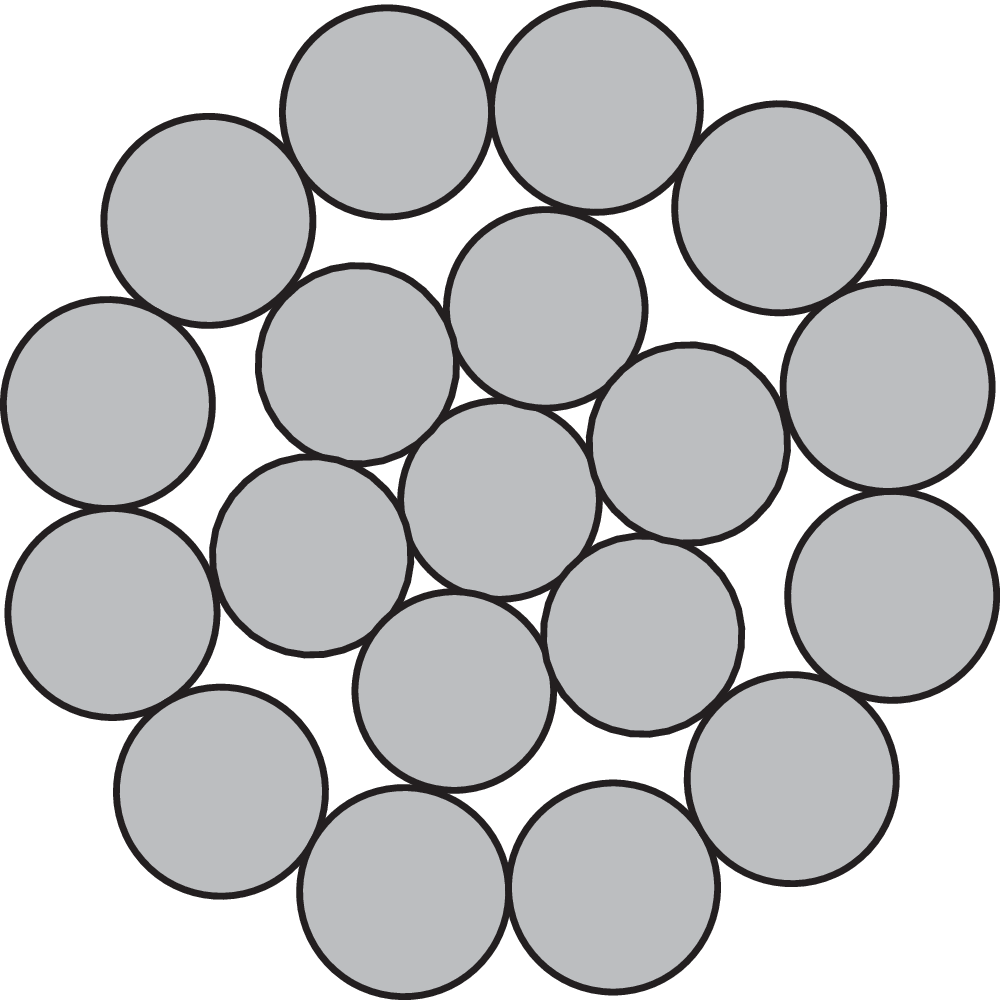
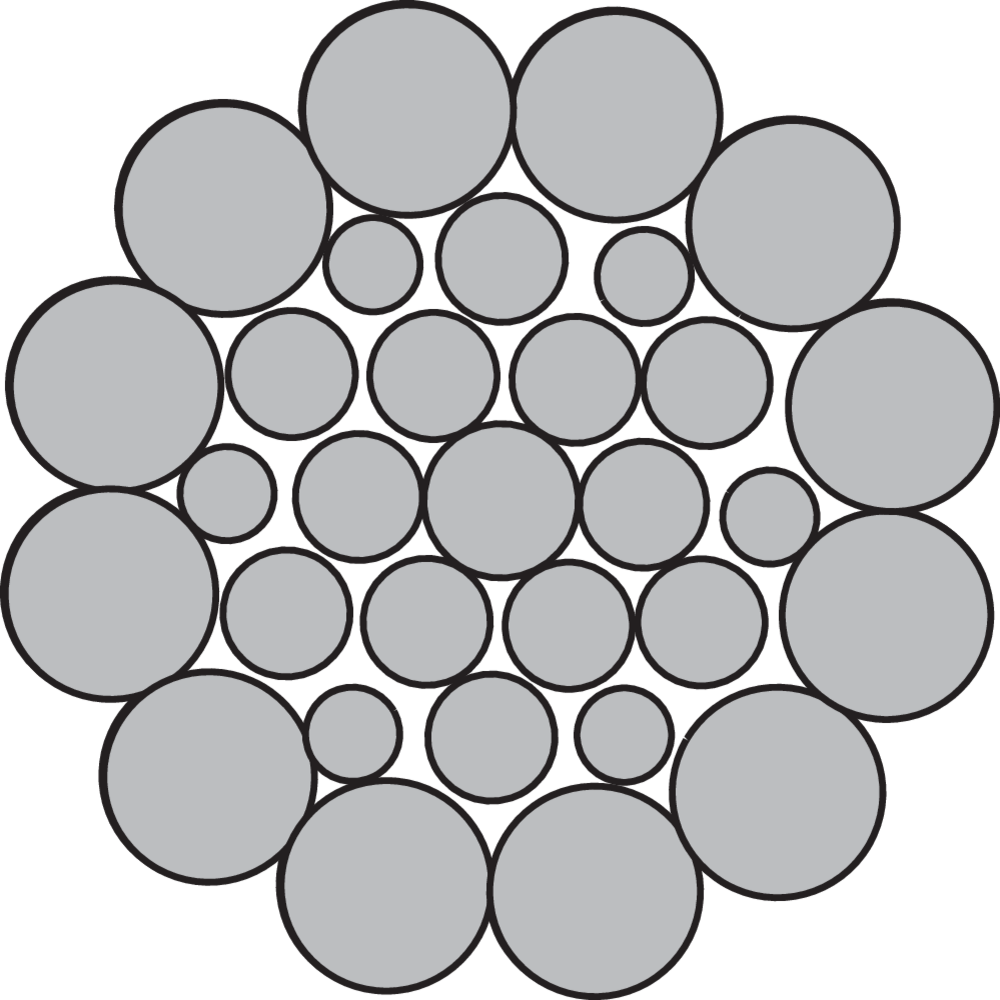
Types of steel wire rope strands
The strand is built up by individual wires which are laid around the core in one or more layers, typically to one of the following constructions:
Ordinary:
Ordinary lay wires - all wires are in the same size.
Seale (S):
Parallel lay wires - different size, same number of wires in outer and inner layer.
Warrington (W):
Parallel lay wires - the outer layer of wires has two different sizes, twice as many outer wires as inner wires.
Warrington-Seale (WS):
Parallel lay wires - a combination between Seale and Warrington, with three or more layers of wire.
Filler wire (F):
Parallel lay wires - twice as many outer wires as inner wires, with small wires to fill the spaces between the large wires.
Compacted strand:
A strand that has been formed through compaction maintaining the steel area whilst increasing the fill factor.
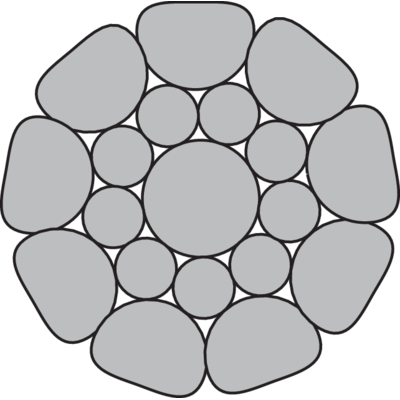
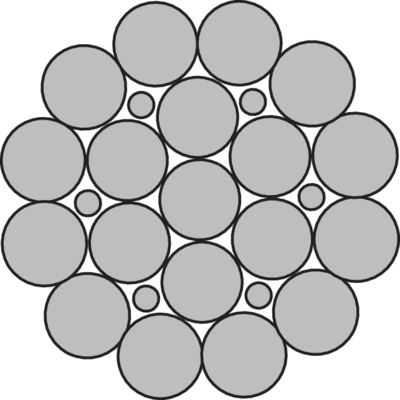
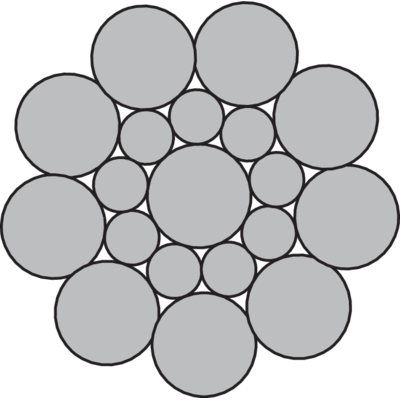
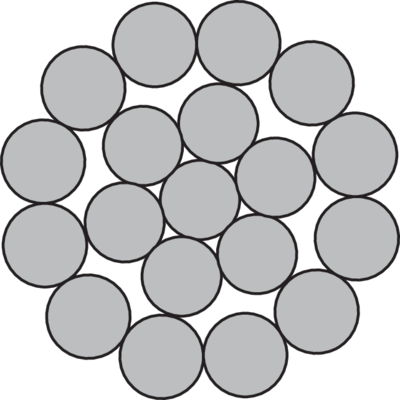
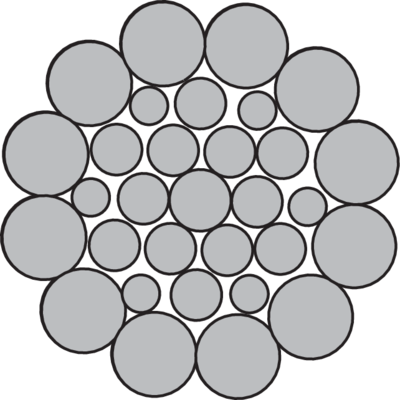
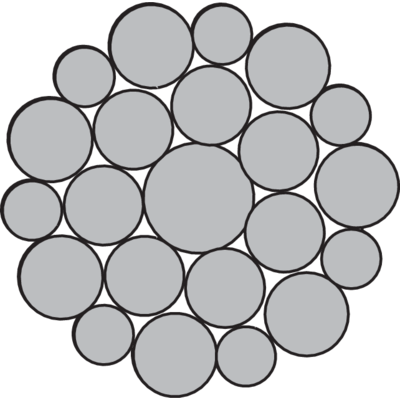



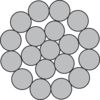







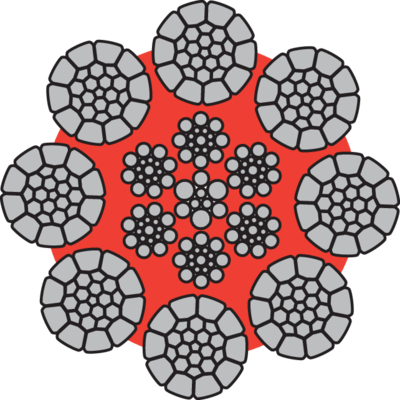
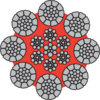
Types of steel wire rope cores
The strands in a rope are laid around a core of either fibre, steel or solid plastic.
Where the strands are laid over a fibre core FC is used, e.g. 6x19-FC.
Ropes with steel cores should be chosen if the rope is exposed to high working temperature, hard strains, high work rate, hard pressures on drums and blocks etc. The steel core gives better support for the strands, which result in the rope retaining its shape better and giving a better distribution of the stresses in the individual wires.
If the steel core of the rope consists of a single strand the term -WSC is used, e.g. 6x19-WSC.
If the steel core of the rope consists of a steel wire rope the term -IWRC is used, e.g. 6x19-IWRC.
Some steel wire ropes can have a plastic encapsulated core which provides increased stability to the rope and also reduces the wear and corrosion in and around the core, e.g. Dyform 8 PI.










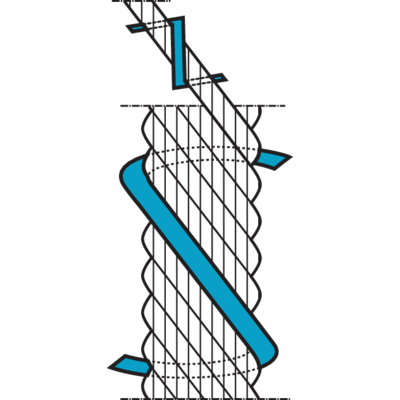
Types of steel wire rope lays
Ordinary hand lay
The direction of the lay of the outer layer of wires in the strands is opposite to the direction of lay of the strands in the rope. Ordinary lay is more resistant to kinking and untwisting, and less likely to fail as a result of crushing and distortion.
Lang's lay
The direction of lay of the outer layer of wires in the strands are in the same direction of lay of the strands in the rope. The advantage of using Lang's lay is that the rope offers a better wearing surface when in use, and therefore can be expected, in many cases to last longer. Lang's lay ropes produce relatively high torque values under working conditions and must not be used on applications where one end of the rope is free to rotate or where problems from rope turn are likely to occur.
Right hand lay
The strands are twisted to the right around the core. Right hand lay is the most common lay direction in a rope.
Left hand lay
The strands are twisted to the left around the core.
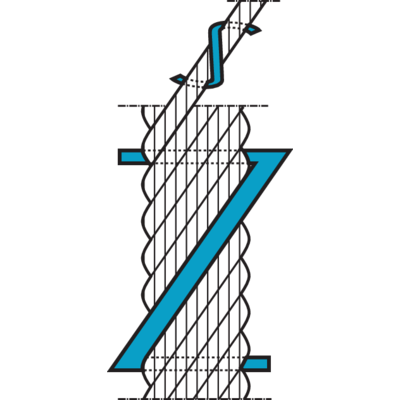
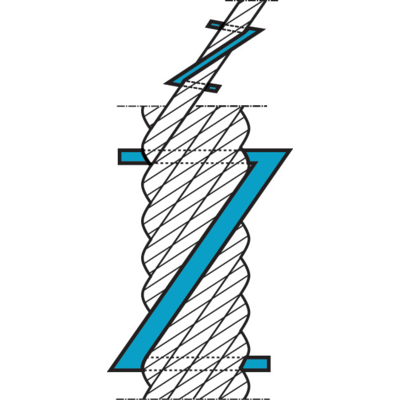
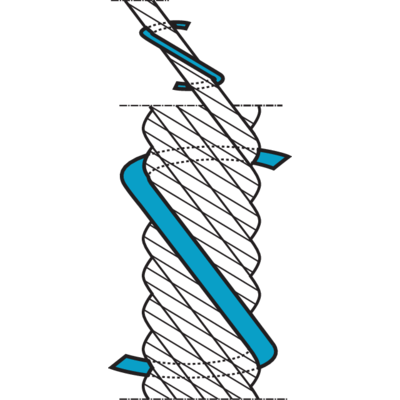
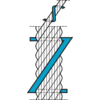
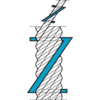
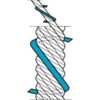




Steel wire ropes with rotation resistant properties
To minimise the tendency to rotate especially with high lifting heights "rotation resistant" or "Low Rotation" ropes should be used.
Rotation resistant ropes are made out of many layers of strands. Every layer is laid in the opposite direction to the next layer, so that the torque in the different layers balances the opposing forces in the rope.



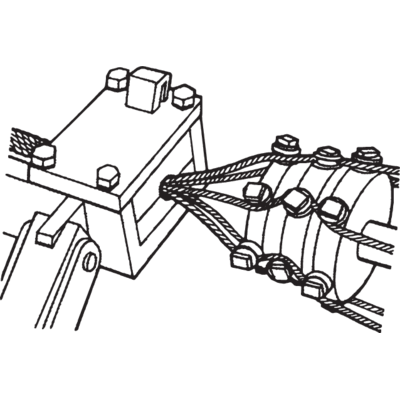
Why is preforming important?
Preforming is a process that puts a helix in the strands to match the helical shape it will assume in the finished rope. Advantages of preforming include:
– The ropes are free from liveliness and twisting tendencies allowing easier installation and handling.
– The ropes can be cut with minimal seizing as exposed ends will not untwist.
Preforming takes place in a preformhead where the strand pass immediately before the closing operation.


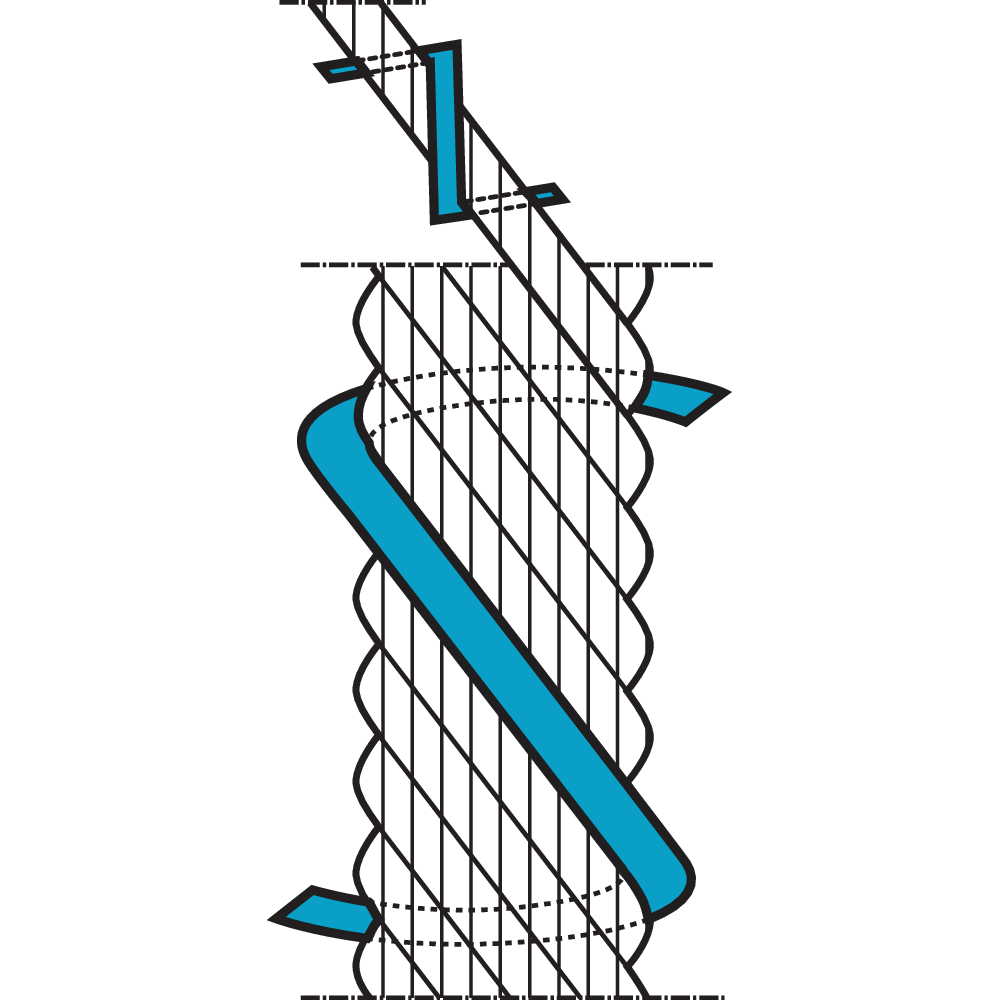
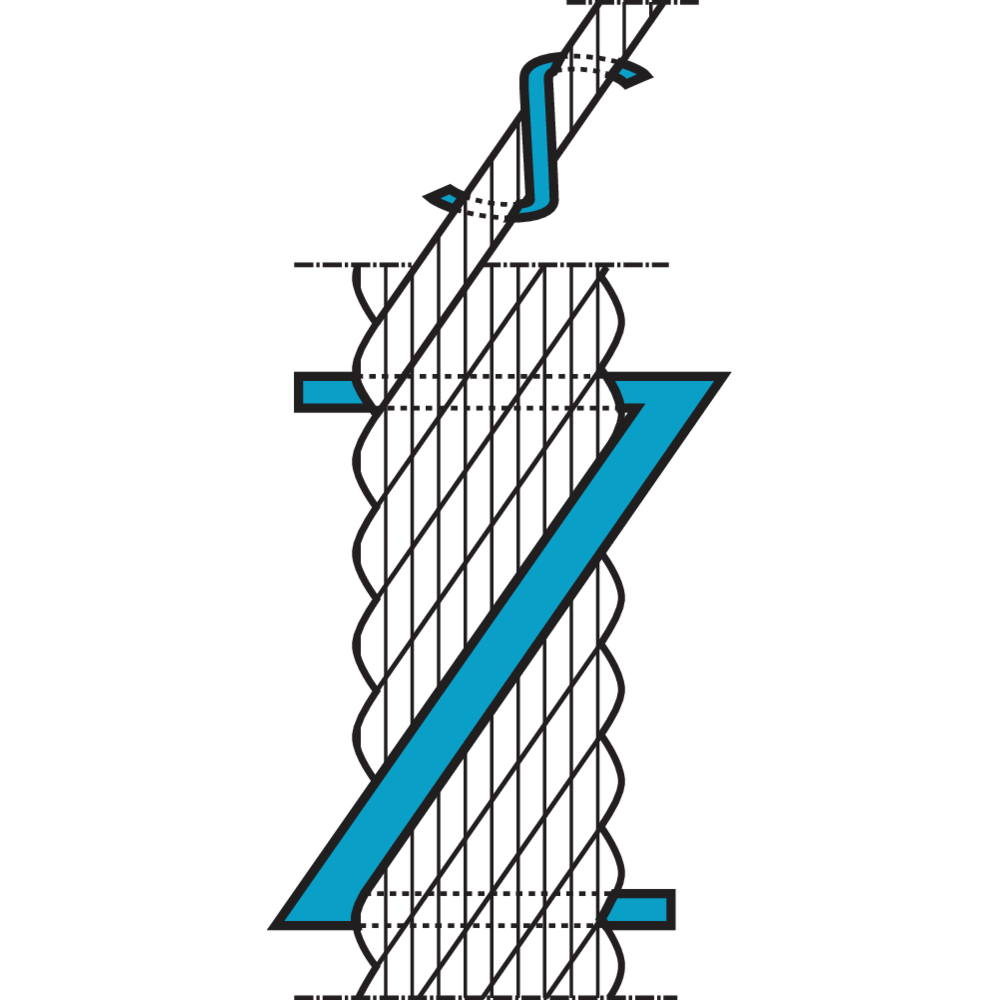
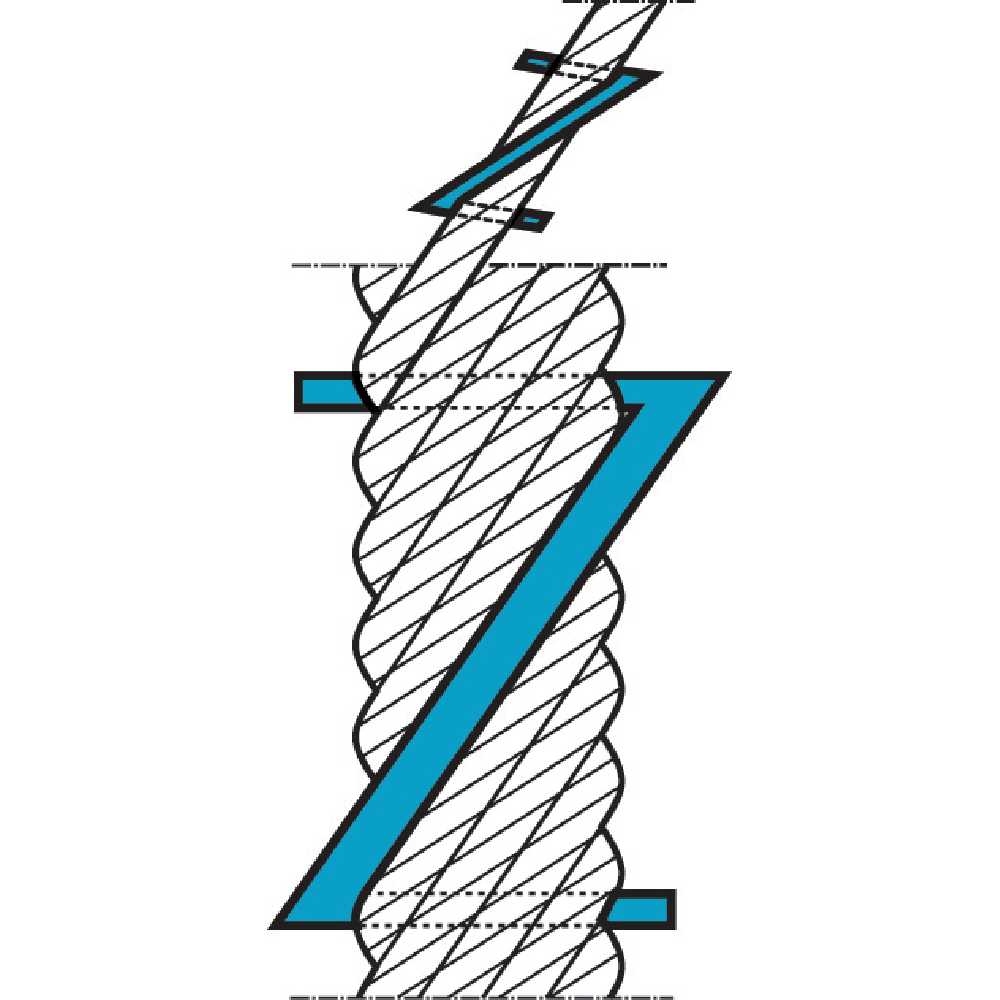
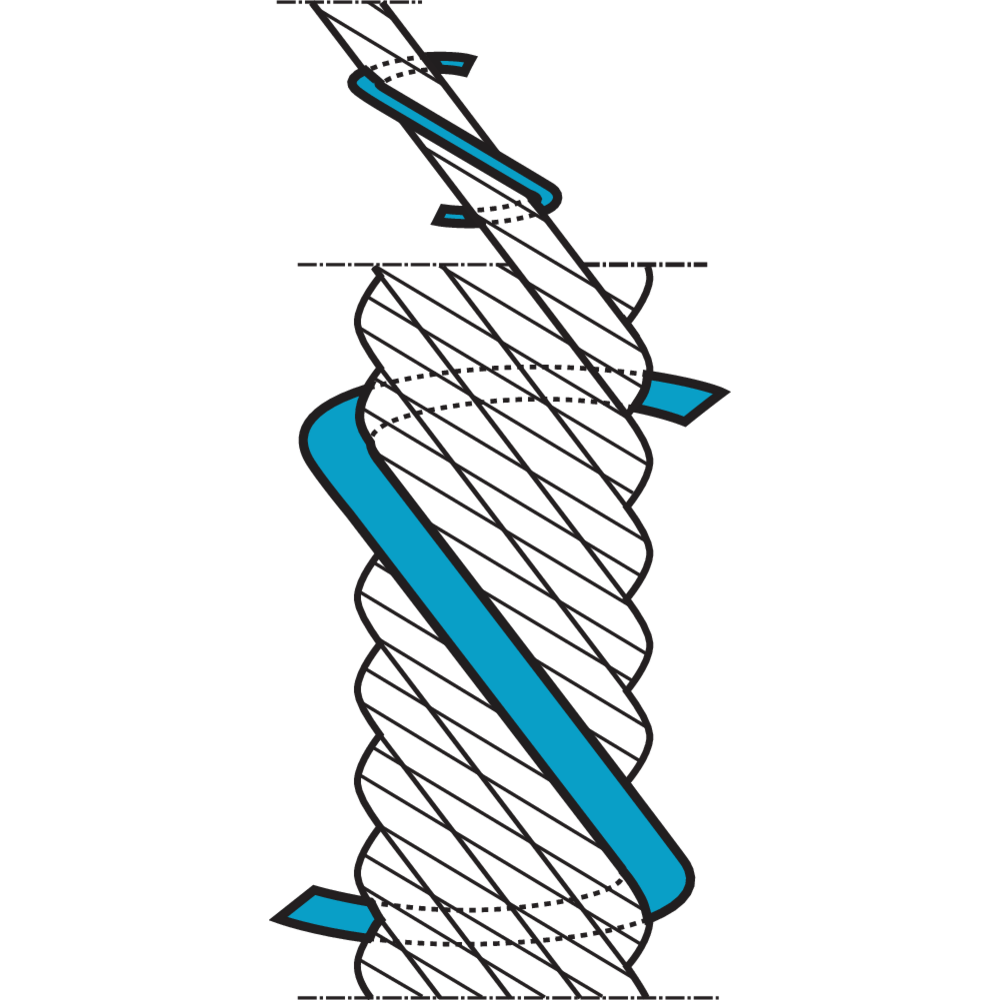
Steel wire ropes lay length
Lay length is the term used for the length of a "wire- or strand helix". Lay length is determined for each wire rope construction and has to be retained, otherwise the life of the wire rope is considerably reduced.
![Strand lay length_eng[new]_225mm_2](/sites/certex-lv/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/Steel%20wire%20rope/Steel%20Wire%20Rope%20-%20Data%20sheet/11515/image-thumb__11515__general-base/strand-lay-length-_converte-new-.6207213b.png)
![Strand lay length_eng[new]_225mm_2](/sites/certex-lv/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/Steel%20wire%20rope/Steel%20Wire%20Rope%20-%20Data%20sheet/11515/image-thumb__11515__general-thumb/strand-lay-length-_converte-new-.0e8a7460.png)
![Strand lay length_eng[new]_225mm_2](/sites/certex-lv/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/Steel%20wire%20rope/Steel%20Wire%20Rope%20-%20Data%20sheet/11515/image-thumb__11515__general-base/strand-lay-length-_converte-new-.6207213b.png)
Minimum and calculated breaking load
The Minimum breaking force (minimum breaking load), in kilonewtons, is the lowest breaking strain of the rope when tested to destruction.
The value calculated from the product of the sum of the crossectional metallic areas of all the individual wires in the rope and the tensile strength grade(s) of the wires. The total metallic area is directly proportional to the square of the nominal diameter of the rope. A standard spinning loss factor that results from the twisting of strands and wire is then applied.


Do you have any questions?
If you have any additional questions, please contact us and we will answer you.





![Strand lay length_eng[new]_225mm_2](/sites/certex-lv/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/Steel%20wire%20rope/Steel%20Wire%20Rope%20-%20Data%20sheet/11515/image-thumb__11515__product-large/strand-lay-length-_converte-new-.39628341.png)



